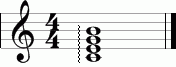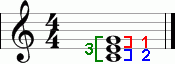Intervalų inversija arba magija solfedžio pamokose

Intervalų inversija – tai vieno intervalo pavertimas kitu, pertvarkant viršutinį ir apatinį garsus. Kaip žinote, apatinis intervalo garsas vadinamas jo pagrindu, o viršutinis – viršutiniu.

O jei sukeisite viršų ir apačią, arba, kitaip tariant, tiesiog apverssite intervalą aukštyn kojomis, tai rezultatas bus naujas intervalas, kuris bus pirmojo, originalaus muzikinio intervalo inversija.

Kaip atliekamos intervalų inversijos?

Pirma, mes analizuosime manipuliacijas tik paprastais intervalais. Konversija atliekama perkeliant apatinį garsą, tai yra pagrindą, grynąja oktava aukštyn arba apatinį intervalo garsą, tai yra viršutinį, oktava žemyn. Rezultatas bus toks pat. Tik vienas iš garsų juda, antrasis lieka savo vietoje, jo liesti nereikia.

Pavyzdžiui, paimkime didelį trečdalį „do-mi“ ir apverskime jį bet kokiu būdu. Pirmiausia „do“ bazę perkeliame oktava aukštyn, gauname „mi-do“ intervalą – mažą šeštą. Tada pabandykime daryti priešingai ir viršutinį garsą „mi“ perkelkime oktava žemyn, todėl taip pat gausime mažą šeštąją „mi-do“. Paveiksle garsas, kuris lieka vietoje, paryškintas geltonai, o oktavą judantis – alyvine spalva.

Kitas pavyzdys: pateikiamas intervalas „re-la“ (tai yra grynas kvintelis, nes tarp garsų yra penki žingsniai, o kokybinė reikšmė yra trys su puse tonų). Pabandykime pakeisti šį intervalą. Perkeliame „re“ aukščiau – gauname „la-re“; arba mes perkeliame "la" žemiau ir taip pat gauname "la-re". Abiem atvejais grynas penktas virto grynu ketvirtu.

Beje, atlikdami atvirkštinius veiksmus, galite grįžti prie pradinių intervalų. Taigi, šeštąjį „mi-do“ galima paversti trečiuoju „do-mi“, nuo kurio pirmiausia pradėjome, tačiau ketvirtąjį „la-re“ galima nesunkiai paversti atgal į penktą „re-la“.

Ką tai sako? Tai rodo, kad tarp skirtingų intervalų yra tam tikras ryšys ir kad yra abipusiai grįžtamų intervalų poros. Šie įdomūs stebėjimai sudarė intervalų inversijų dėsnių pagrindą.

Intervalų apsisukimo dėsniai

Žinome, kad bet kuris intervalas turi dvi dimensijas: kiekybinę ir kokybinę reikšmę. Pirmoji išreiškiama kiek žingsnių apima tas ar kitas intervalas, žymimas skaičiumi, nuo jo priklauso intervalo pavadinimas (prima, antras, trečias ir kt.). Antrasis nurodo, kiek tonų ar pustonių yra intervale. Ir jo dėka intervalai turi papildomus paaiškinančius pavadinimus iš žodžių „grynas“, „mažas“, „didelis“, „padidintas“ arba „sumažintas“. Pažymėtina, kad priėjus keičiasi abu intervalo parametrai – ir žingsnio indikatorius, ir tonas.

Yra tik du įstatymai.

1 taisyklė. Apverčiant grynieji intervalai išlieka gryni, maži virsta dideliais, o dideli, priešingai, mažais, sumažėję intervalai didėja, o padidinti, savo ruožtu, sumažėja.

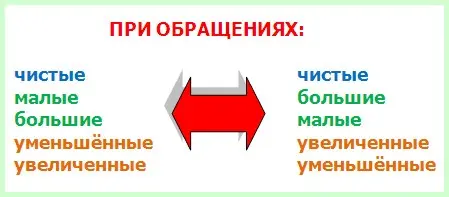
2 taisyklė. Primos virsta oktavomis, o oktavos – primomis; sekundės virsta septintomis, o septintos sekundėmis; trečdaliai tampa šeštaisiais, o šeštieji – trečdaliais, kvartai – penktomis, o penktos – atitinkamai ketvirtomis.

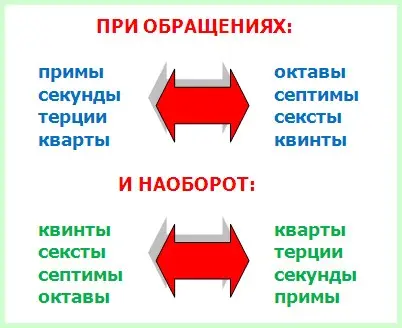
Abipusiai invertuojančių paprastų intervalų žymėjimų suma lygi devyniems. Pavyzdžiui, prima žymima skaičiumi 1, oktava – skaičiumi 8. 1+8=9. Antras – 2, septintas – 7, 2+7=9. Treciai – 3, šeštokai – 6, 3+6=9. Kvartalai – 4, penktadaliai – 5, kartu vėlgi pasirodo 9. Ir, jei staiga pamiršai, kas kur eina, tiesiog iš devynių atimk tau duotą intervalo skaitinį žymėjimą.

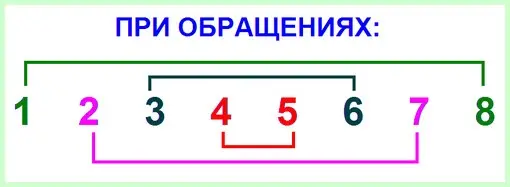
Pažiūrėkime, kaip šie įstatymai veikia praktiškai. Pateikiami keli intervalai: gryna prima iš D, mažoji trečdalis iš mi, pagrindinė sekundė iš C aštrumo, sumažinta septinta iš F, padidinta ketvirta iš D. Apverskime juos ir pamatysime pokyčius.

Taigi po konvertavimo grynoji prima iš D virto grynąja oktava: taip pasitvirtina du taškai: pirma, grynieji intervalai išlieka gryni ir po konvertavimo, antra, prima tapo oktava. Toliau mažasis trečiasis „mi-sol“ po konversijos pasirodė kaip didelis šeštasis „sol-mi“, kuris vėl patvirtina mūsų jau suformuluotus dėsnius: mažas išaugo į didelį, trečiasis tapo šeštu. Toks pavyzdys: didžioji sekundė „C-sharp ir D-sharp“ pavirto į mažą septintąją tų pačių garsų (maža – į didelį, antroji – į septintąją). Panašiai ir kitais atvejais: sumažinimas padidėja ir atvirkščiai.

Išbandyk save!

Siūlome šiek tiek pasipraktikuoti, kad geriau įtvirtintume temą.

PRATIMAS: Atsižvelgiant į intervalų seriją, turite nustatyti, kas yra šie intervalai, tada mintyse (arba raštu, jei sunku taip iš karto) juos paversti ir pasakyti, į ką jie pavirs po konversijos.

Fokusuoja su sudėtiniais intervalais

Sudėtiniai intervalai taip pat gali dalyvauti apyvartoje. Prisiminkite, kad intervalai, platesni už oktavą, tai yra none, decims, undecims ir kiti, vadinami sudėtiniais.

Norėdami gauti sudėtinį intervalą, kai jis apverstas iš paprasto intervalo, turite vienu metu perkelti ir viršų, ir apačią. Be to, pagrindas yra oktava aukštyn, o viršuje - oktava žemyn.

Pavyzdžiui, paimkime didžiąją trečdalį „do-mi“, bazę „do“ pakelkime oktava aukščiau, o viršutinę „mi“ – atitinkamai oktava žemiau. Dėl šio dvigubo judesio gavome platų intervalą „mi-do“, šeštą per oktavą arba, tiksliau, mažą trečią dešimtainį.

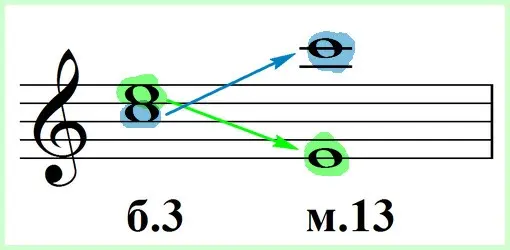
Panašiai kiti paprastieji intervalai gali būti paversti sudėtiniais intervalais, ir atvirkščiai, paprastas intervalas gali būti gaunamas iš sudėtinio intervalo, jei jo viršus nuleidžiamas oktava, o pagrindas pakeltas.

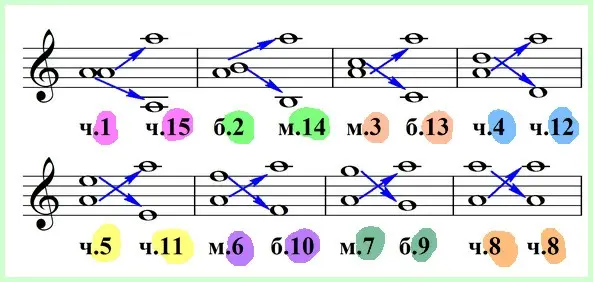
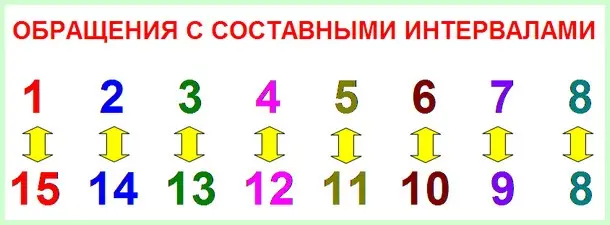
Kokių taisyklių bus laikomasi? Dviejų tarpusavyje apverčiamų intervalų pavadinimų suma bus lygi šešiolikai. Taigi:

• Prima virsta kvintdecima (1+15=16);
• Antrasis virsta ketvirtadaliu (2+14=16);
• Trečias pereina į trečią kablelį (3+13=16);
• Kvartas tampa duodecima (4+12=16);
• Kvinta persikūnija į undecimą (5+11=16);
• Sexta virsta kableliu (6+10=16);
• Septima pasirodo kaip nona (7+9=16);
• Šie dalykai neveikia su oktava, ji virsta savimi ir todėl sudėtiniai intervalai neturi nieko bendra, nors ir šiuo atveju yra gražių skaičių (8+8=16).

Intervalų inversijų taikymas

Jūs neturėtumėte galvoti, kad intervalų inversija, taip išsamiai išnagrinėta mokykliniame solfedžio kurse, neturi praktinio pritaikymo. Atvirkščiai, tai labai svarbus ir reikalingas dalykas.

Praktinė inversijų apimtis susijusi ne tik su supratimu, kaip atsirado tam tikri intervalai (taip, istoriškai kai kurie intervalai buvo atrasti inversijos būdu). Teorinėje srityje inversijos labai padeda, pavyzdžiui, įsimenant vidurinėje ir kolegijoje studijuotus tritonus ar charakteringus intervalus, suvokiant tam tikrų akordų sandarą.

Jei imtume kūrybos sritį, tai apeliacijos plačiai naudojamos kuriant muziką, o kartais jų net nepastebime. Paklausykite, pavyzdžiui, gražios romantiškos dvasios melodijos gabalo, visa tai pastatyta ant kylančių trečdalių ir šeštų intonacijų.

Beje, jūs taip pat galite nesunkiai pabandyti sukurti kažką panašaus. Net jei imtume tas pačias trečdalius ir šeštąsias, tik mažėjančia intonacija:

PS Mieli draugai! Šia pastaba baigiame šios dienos epizodą. Jei turite daugiau klausimų apie tarpų inversijas, užduokite juos šio straipsnio komentaruose.

PPS Galutiniam šios temos įsisavinimui siūlome pažiūrėti juokingą filmuką iš nuostabios mūsų dienų solfedžio mokytojos Anos Naumovos.